رسم مربع بواسطة OpenGL : دورة OpenGL لغة c++ الدرس الخامس

رسم مربع بواسطة OpenGL يتطلب الإلمام ببعض المهام الرئيسية التي قمنا بتنفيذها في الدرس السابق. حيث أن الطريقة ليست مختلفة كثيرًا لكنها تتطلب المعرفة بأساسيات الرسم. وبالتالي فإن عملية الإستدعاء تطلب زيادة في عدد الإحداثيات التي ستتضح فيما بعد أنها عبارة عن مثلثين بــ6 أضلاع.

وكذلك الأمر بالنسبة لمكونات EBO (Element buffer object).^[1]سنتمكن من رسم مربع بواسطة OpenGL عن طريق دمج مثلثين من الإحداثيات. حيث أن كافة النماذج المتعلقة بالرسم ستتكون لاحقًا عن طريق علم المثلثات.

جدول المحتويات

1. رسم مربع بواسطة OpenGL
   1. تكوين EBO (Element Buffer Object)
      1. تعريف EBO في الشيفرة
         1. المراجع

رسم مربع بواسطة OpenGL

يتطلب منا ذلك تعيين بعض الإحداثيات التي أجريناها على درس المثلثات. حيث أن منها مثلث قديم تم التعديل على طول أضلاعه لكي نتمكن من إخراج النتيجة على النحو المطلوب.[1] نقوم الآن بإجراء التعديل اللازم على الشيفرة وذلك باستبدال الإحداثيات السابقة لمصفوفة vertices.[1]

GLfloat vertices[] = {
// First triangle
0.5f, 0.5f, 0.0f, // Top Right
0.5f, -0.5f, 0.0f, // Bottom Right
-0.5f, 0.5f, 0.0f, // Top Left
// Second triangle
0.5f, -0.5f, 0.0f, // Bottom Right
-0.5f, -0.5f, 0.0f, // Bottom Left
-0.5f, 0.5f, 0.0f // Top Left
};

كما تشاهد مصفوفة الأحداث في الأعلى , فهي الجزء المسؤول عن رسم مربع بواسطة OpenGL. حيث أن أول ثلاث إحداثيات تشكل المثلث الأعلى الأيمن. بينما آخر ثلاث إحداثيات ستشكل المثلث السفلي الأيسر. بالتالي نحصل على 6 مواقع إحداثيات أساسية لكل مربع يتم تكوينه في جميع رسومات الحاسوب.  

تكوين EBO (Element Buffer Object)

عند رسم مربع بواسطة OpenGL باستخدام الطريقة السابقة , فإن ذلك ممكنًا ولكن يتطلب مضاعفة في عملية الرسم مع عدم وجود خطة واضحة بشأن الإحداثيات الكبيرة مما يقود إلى بطئ في المضلعات المتعددة. ولذلك يعود الفضل لـ EBO في تقديم خطة واضحة لبطاقة العرض , يتم من خلالها معرفة خريطة القلم.[1]

على سبيل المثال , إن أفضل تعبير لعملية الرسم هو أن هناك قلم بالفعل يريد معطيات الرسم قبل أن يبدأ رحلته.[1] يقدم لك مخزن EBO مصفوفة تدل على إحداثيات مربع بالفعل , لكن معالجتها ستتم عبر المثلثات. ما يعني أن شيفرة الإحداثيات ستتكون من متغيرين. الأول مصفوفة بأربع إحداثيات والثاني هو مصفوفة تحدد مؤشرات الرسم.

GLfloat vertices[] = {
0.5f, 0.5f, 0.0f, // Top Right
0.5f, -0.5f, 0.0f, // Bottom Right
-0.5f, -0.5f, 0.0f, // Bottom Left
-0.5f, 0.5f, 0.0f // Top Left
};
GLuint indices[] = { // Note that we start from 0!
0, 1, 3, // First Triangle
1, 2, 3 // Second Triangle
};

لو قمنا بالتركيز بعناصر المتغير indices سنجد بأن هناك نقطة تلاقي بين المثلثين(عامل مشترك) وهي الرقم 1. والتي تدل فعليًا على إحداثيات Bottom right. ما يعني أن القلم سيبدأ برسم المثلث الثاني من إحداثيات أسفل يمين الفضاء.

تعريف EBO في الشيفرة

إن رسم مربع بواسطة OpenGL يتطلب تعريف متغير EBO في الشيفرة الخاصة بنا ليصبح شكل المتغيرات على النحو التالي:

GLuint EBO;
glGenBuffers(1, & EBO);

بطريقة مشابهة لكائن VBO سنقوم الآن بربط EBO مع الإشارة إلى indices بمتغيرات الدالة لتصبح تمامًا كما يلي:

glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO); -hj
glBufferData(GL_ELEMENT_ARRAY_BUFFER, sizeof(indices), indices,
GL_STATIC_DRAW);

نلاحظ الآن بأننا نعطي GL_ELEMENT_ARRAY_BUFFER قيمة EBO التي قمنا بملئها مسبقًا ويتبقى لدينا استبدال الدالة glDrawArrays لتحل glDrawElements مكانها تمامًا مثل الشيفرة التالية:

glBindBuffer(GL_ELEMENT_ARRAY_BUFFER, EBO);
glDrawElements(GL_TRIANGLES, 6, GL_UNSIGNED_INT, 0);

عند رسم مربع بواسطة OpenGL و EBO سيتسنى لنا ملئ القيم كما في الشيفرة السابقة. القيمة الأولى توفر لنا نوع النمط الذي نريد استخدامه وهو مثلثات والقيمة الثانية هي عدد المؤشرات التي نريد التوصيل بينها indices.^[1] والقيمة الثالثة تدل على نوع المتغير وهو بالطبع GL_UNSIGNED_INT ما يسمح بقراءة قيم EBO السالبة.^[1]

يتم الإبقاء على قيمة الإزاحة 0 كما هي.^[1] الآن وبعد تطبيق كافة الخطوات السابقة ستظهر لنا نتيجة الرسم النهائية , كما في الصورة التالية.

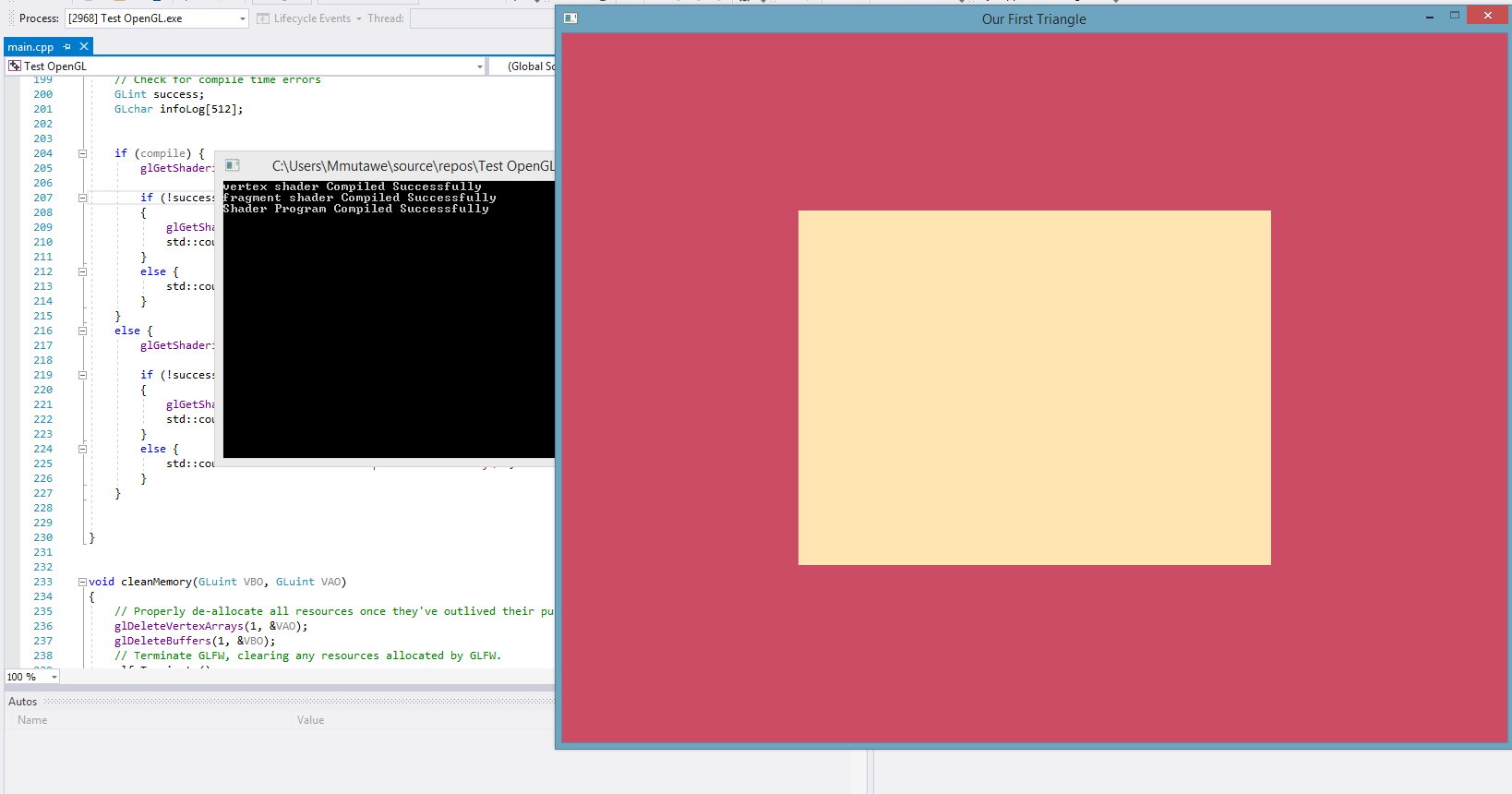
تمت الكتابة بواسطة : محمد

آخر تحديث : لم تخضع لتحديثات بعد